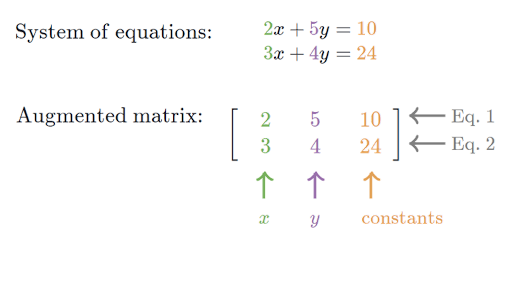Matrix Example Problems With Solution Pdf
For each matrix below determine the order and state whether it is a square matrix. X0 2 4 2 1 4 3 5.
Matrices Algebra All Content Math Khan Academy
Has the property that for every matrix A.

Matrix example problems with solution pdf. Let A 0 2 2 2 2 2 2 2 2 6 1 A. Let Abe an n nskew-hermitian matrix over C ie. Let A X Y be n nmatrices.
Recall from Algebra I that equivalent equations have the same solution set. The given matrix A is diagonalized. These are real problems and they need an answer.
2x 1 6x 3 8 x 2 2x 3 3 3x 1 6x 2 2x 3 4. Example 1 Matrix Equality Let A 79x 0 1 y 1 and B 790 0 111. Able to develop bus admittance matrix to solve power flow solution.
Matrix multiplication Defining the problem Setting up the equations Arranging the equations in matrix form Solving the equations Meaning of the solution Examples Geometry Balancing chemical equations Dimensional analysis. AThe resulting row echelon form of this 3 5 matrix is 2 4 3 5. In a matrix eigenvalue problem the task is to determine λs and xs that satisfy 1.
They are connected by p. M displaystyle m m is the number of columns. A matrix A having same numbers of rows and columns is called a.
BThe resulting reduced row echelon form is 2 4 3 5. 4 Problems and Solutions and nd the eigenvalues and eigenvectors of this matrix. The row rank is the maximum number of linearly independent rows.
A square matrix Aover C is called skew-hermitian if A A. We could then state. When the length of e is as small as possible bx is a least squares solution.
This section emphasizes bx the least squares solution. Let A 2 4 6 3 2 4 1 2 13 9 3 3 5. B Find the general solutions of dx dt Ax.
It is therefore straightforward to nd the solution of the system. In this case the matrix of the example is 4 5 displaystyle 4 times 5 4 5 because it has 4 displaystyle 4 4 rows and 5 displaystyle 5 5 columns. Consider the matrix A given by Using the three elementary row operations we may rewrite A in an echelon form as or continuing with additional row operations in the reduced row-echelon form From the above the homogeneous system has a solution that can be read as.
Show that B U AUis a skew-hermitian matrix. Our goal in this section is to computebx and use it. Rank Row-Reduced Form and Solutions to Example 1.
This is a matrix called the inverse matrix and we must understand the following work in order to find it. X is an exact solution to Ax Db. A square matrix has the number of rows equal to the number of columns.
Mxn A O O A A. A matrix eigenvalue problem considers the vector equation 1 Ax λx. To solve the first equation we write a sequence of equivalent equations until we arrive at an equation whose solution set is obvious.
The problem is finding the matrix B such that AB I. The solutions are x 1t 12t t for t R. Let U be an n n unitary matrix ie U U 1.
A PDP 1 with P 2 4 1 1 12 1 2 12 1 1 1 3 5. 2 4 1 0 17 0 0 1 5 0 0 0 0 1 3 5 So since the last row gives the equation 0 1 this system is inconsistent. Xz 1 x2y 3z 11.
3Solve the following system of equations. 7Consider the following system of equations. The row rank and the column rank of Xare equal called the rank of X.
Show that such a matrix is normal ie we have AA AA. Solution of Simultaneous Linear Equations AXB Preliminary. Number of rows and columns are not equal therefore not a square matrix.
X y 3z 3 2x z 0 2y 7z c aFor what values of cdoes the system have a solution. Is a zero matrix of order 2 x 4. Suppose that we had a matrix B such that AB I The unit matrix.
The steps of adding 1 to both sides of the first equation and of dividing both. We have etA PetDP 1 2 4 1 1 12 1 2 12 1 1 1 3 5 2 4 et 0 0 0 e2t 0 0 0 e t 3. The dimensions of the matrices are n m displaystyle ntimes m n m where.
Exercise 62 We start again by writing down the matrix of coe cients for this system. Bus admittance matrix Ybus. Notice that the matrix of coe cients is equal to matrix M 1 whose inverse was computed in E31.
Since x 0 is always a solution for any and thus not interesting we only admit solutions with x 0. 2 Problems and Solutions Problem 4. I Let X be an m nmatrix.
Speci cally X M 1 1 B 0 x y z 1 A 1 3 0 3 6 0 0 3 0 0 1 1 1 A 0 3 7 9 1 A 0 11 7 3 1 A which implies that x 11. In this example since there is no connection between bus 1 and 4 Y 14 Y 41 0 similarly Y 24 Y 42 0. Solution For the two matrices to be equal we must have corresponding entries equal so x 0 a 13 b 13 y 1 11 or y 10 a 23 b 23 quick Examples Row Matrix Column Matrix and Square Matrix A matrix with a single row is called a row matrixor row vector.
R2 R2 denote rotation counterclockwise about the origin in R2 by π 4 radians or 45. Here A is a given square matrix λan unknown scalar and x an unknown vector. Putting the coe cients into a matrix we obtain the augmented matrix.
For example O 0000 0000 ªº ¼. 7 points Let T. 2 4 0 1 5 4 1 4 3 2 2 7 1 2 3 5 Now we put this matrix into reduced row echelon form and obtain.
This distinguishes zero matrix from the real number 0. 10 points Solve the following system of linear equations. ABX I X B b X B b This gives a numerical solution for X.
Find the values of x and y such that A B. The previous section emphasized p the projection. D 2 4 1 0 0 0 2 0 0 0 1 3 5.
C Solve the initial value probelm dx dt Ax. The column rank of X is the maximum number of linearly independent columns. Zero matrices are generally denoted by the symbol O.
2x 15 2x 15 2x 6 x 3 Solution set is 3. CThe solution for 1 is and the solution for 2 is. The solutions are x 1t y 52t z t for t R.
ANALYSIS- Power flow solution Ybus Expected Outcomes. N displaystyle n n is the number of rows and.

Matrix Multiplication Pdf Math Humor Eureka Math Algebra

Matrix Operations Algebra 2 Worksheet Printable Algebra 2 Worksheets Matrix Multiplication Word Problem Worksheets

3 4a Matrix Operations Finite Math

Types Of Matrices With Examples Matrix Type Example

Matrix Mathematics Matrix Multiplication Matrix Common Core Math Standards

Pin On Matematica Aritmetica E Algebra

The Matrix And Solving Systems With Matrices She Loves Math Matrices Math Exponent Worksheets Math

Matrix Matrices Foldable Graphic Organizer Interactive Notebook Matrices Math Studying Math Mathematics Worksheets

Ncert Solutions For Class 12 Maths Chapter 3 Exercise 3 2 Matrices Math Class 12 Maths Math Exercises

Gaussian Elimination Method Gauss Elimination Method Engineering Mathematics Math Vector Math Notes Mathematics

3 4a Matrix Operations Finite Math

Solution Selection Matrix Goleansixsigma Com Business Analysis Solutions Lean Six Sigma

Pin On Secondary Math Interactive Notebook Ideas
Representing Linear Systems With Matrices Article Khan Academy

Solving Linear Systems Using Matrices Youtube

Matrices And Determinants Miscellaneous Problems Problem Questions With Answer Solution Business Mathematics

Linear Algebra Example Problems Solving Systems Of Equations 2 3 Youtube